I know this been hashed over a few times on this forum, but after my misreading / misunderstanding of a recent post, I had put together some information that someone (especially a newer bass player) may find useful. As people process information and learn differently, I figured I’d share some information that helped me with my personal understanding of some important musical concepts.
When musicians refer to Degrees, it is very important to understand the context from which the speaker is speaking, otherwise its very easy for the listener or student to get confused.
The first way of describing degrees is to refer to each note in terms of its POSITION in the Major scale. For example in a C Major Scale, we have the following notes: C, D, E, F, G, A, B, (C). In this method of describing a scale we will assign a number or designation to each note in the scale, starting with the first note, in this case “C”. For example: C (Root or 1), D (2 or 2nd), E (3 or 3rd), F (4 or 4th), G (5 or 5th), A (6 or 6th), B (7 or 7th), C (Octave or Root again). As shown below in the basic “box pattern” of a major scale.
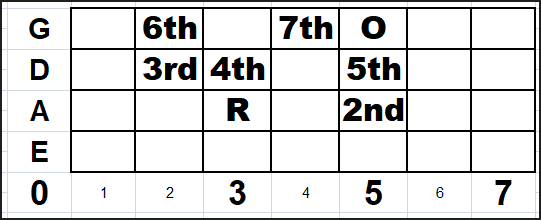
So far so good, and I hope not too confusing. Using this method, other scales or modes are often described in relation to the shared Root note Major scale. Say for example someone using this method would like to describe the pattern of a C minor scale (C, D, Eb, F, G, Ab, Bb, (C)) it would be described in terms of its relation to the C Major scale. So in a C minor scale we can see that the E is flat (1 half step or fret lower), the A is flat and the B is flat in comparison to the C Major Scale.
This is pretty easy to visualize. Most beginner players know (or will know it after a couple lessons) the “box pattern” of the Major scale. If you tell that player to flat the 3rd, the 6th and the 7th notes, you are telling them to take the Major scale that they know and adapt it to a new scale pattern starting from the same root. If, you wanted to teach this same student a Dorian scale, you just tell them to flat the 3rd and 7th notes. And so forth. There’s nothing wrong with this approach and makes approaching new scales relatively easy to a beginner, but it can lead to confusion when other degree methods are learned or being utilized.
The second way to describe a degree is in relation of one note to another note IN THAT SCALE. This is similar to what was discussed above, but there are some subtle differences. I’ve always call this Scale Degree in my head, but there’s probably a proper or better name for this. To use this method one simply counts the number of notes (including the starting note) between target note and destination note - giving us a Unity, 2nd, 3rd, 4th, 5th, 6th, 7th and Octave (I don’t believe these terms are generally going to be used outside of a single octave, there’s probably some terminology for this but I’ve not studied that as of yet).
Using this Scale Degree method, with a C Major scale as an example, if we ascend from a C to an E we’ve “gone up a 3rd” and from E to G, again we’ve gone up a 3rd. Ascending from a C to a G we’ve gone up a 5th. Descending works the same way, if we descend from C to G, we’ve gone down a 4th. Ascending by two 3rds is a 5th. And so forth.
If we receive an instruction saying play an ascending C Major scale skipping by 3rds. We can understand that to mean it should be played as such: C followed by E, D followed by F, E followed by G, F followed by A, G followed by B, A followed by C, B followed by D (for sake of completeness), and lastly C. In tab format, it looks like this:

Lastly, we will discuss Intervals.
Intervals are a measurement of distance between 2 different notes chromatically, ascending or descending. This is counted in half steps (each fret), NOT including the note started on.
So, a Chromatic Scale (playing every note from Root to Octave), starting on C ascending = C, C# (Db), D, D# (Eb), E (Fb), F (E#), F# (Gb), G, G# (Ab), A, A# (Bb), B (Cb), and C (B#) - see chart below.
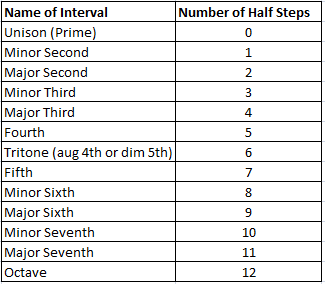
If we take the C Major scale as an example, when describing the Interval between C to G, we are counting # of half-steps (again, not including the starting note). To get from C to G we are ascending 7 half-steps, which is called a (Perfect) Fifth (see chart above). Descending from G to C would be a (Perfect) Fourth. And so on. This is a more precise way of looking at the relation of notes in a scale, because, in this context, if we start on Root C and I tell you to “go a third” I haven’t actually given you any instruction. There’s a Minor Third (3 half steps - which brings us to a D#/Eb) and there’s a Major Third (4 half steps - which brings us to an E) - so, which are you supposed to do? You don’t know with the given information unless you know the way the scale is constructed in terms of Intervals and can imply which of the thirds makes most sense in context.
So, lets take this further. The Major Scale is constructed as follows: Root (C) ascend by a Major Second (D), ascend by a Major Second (E), ascend by a Minor Second (F), ascend by a Major Second (G), ascend by a Major Second (A), ascend by a Major Second (B), ascend by a Minor Second (C).
Or if looked by whole-steps (2 half-steps) and half-steps: W W H W W W H.
Ok, so now this gives us more information to make sense of the short-hand that is often used. In the case of a (Perfect) Fifth for a C Major scale, it would be a G (7 half-steps from first note). Another way of looking at the Fifth in a Major scale is to say it is a Major Third followed by a Minor Third. We can really get deep into the weeds from here, so I leave this as an exercise to explore and discuss.
Below is a picture of a 5 String Bass fret-board showing all valid notes in the key signature of A (shown in red)) and I’ve charted out the number of half-steps from the tonic A up to 12, within 2 complete octaves from pitch A1. Blue boxes represent valid notes in A Major. Half steps go from 0 through 12 ascending, and 0 through -12 descending starting from A2 (second full octave) to better show the Interval relationship between the 0 and ascending or descending from there. So, if starting on 0 and ascending through 7 brings us to a Fifth, but descending from 0 to -5 (5 half steps) brings us to a Fourth. This is a full 12 half steps, which defines the octave. The scale of A Major was chosen on 5 string as it’s the only major scale I could think of that that completes a full -12 to 12 sequence both vertically across 5 frets and horizontally across all 24 frets.
That’s enough for now. I hope some people find it useful.
